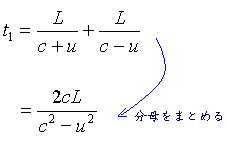 丂嘆
丂嘆丂憡懳榑偺奣梫傪暔棟妛婎慴偲偄偆杮偵廗偭偰傛傝嵱偄偰愢柧偟傑偡丅
側傞傋偔幃傪巊傢側偄偱愢柧偟偨偄偺偱偡偑丄偦偆偡傞偲梋寁偵傢偐傝偵偔偄偲巚傢傟傞偺偱巊偭偰偄傑偡丅
寢峔挿偔側偭偰偟傑偄傑偟偰丄撉傒偵偔偄晹暘傕懡偄偐偲巚偄傑偡偑棟夝偟偰傕傜偊傟偽巇崌偣側偙偲偱偡丅
傑偨丄#偺斣崋偺晅偄偰偄傞傕偺偼曗懌愢柧偑偁傝傑偡偺偱嶲峫偵偟偰壓偝偄丅
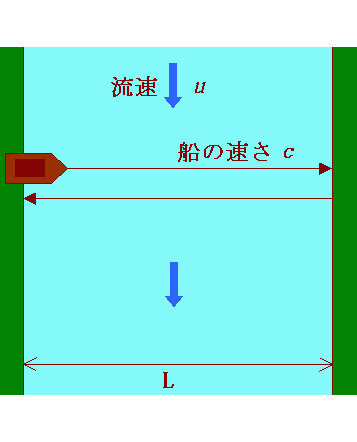
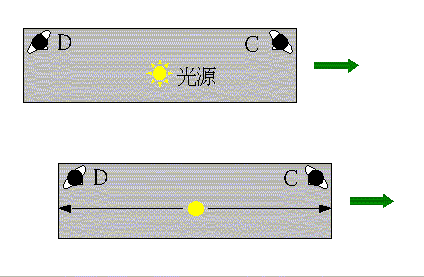
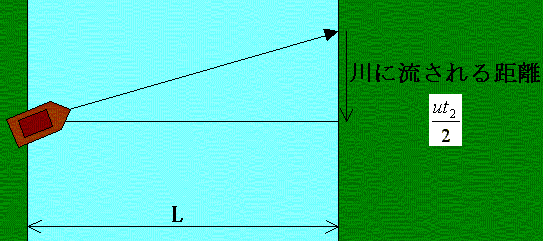
丂僄乕僥儖傪揱傢傞岝偺塣摦偼丄愳傪搉傞慏偺塣摦偵偨偲偊傜傟傞丅
傑偢丄棳傟偺傑偭偨偔側偄壐傗偐側悈忋傪懍偝 c 偱摦偔慏傪峫偊傑偡丅
偙偺慏偑棳懍 u 偺愳傪壓傞偲偒丄娸偵懳偡傞懍偝偼 c + u 丄媡偵偙偺愳傪忋傞偲偒偼 c - u 偲側傝傑偡丅
偙偺慏偑偁傞抧揰偐傜嫍棧 L 偩偗壓偭偰丄傑偨傕偲偺偲偙傠傑偱栠偭偰偔傞偺偵梫偡傞帪娫 t1 偼
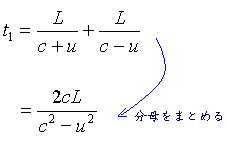 丂嘆
丂嘆
偲側傞丅(恾1嶲徠丅傑偨丄忋幃偑傢偐傜側偄曽偼僋儕僢僋丅#2)
 丂恾1丂丂丂
丂恾1丂丂丂
 丂恾2
丂恾2
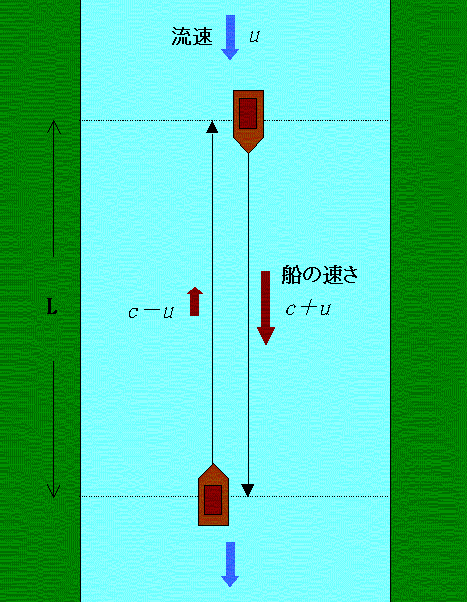
傑偨丄偙偺慏偑暆L偺愳傪墲暅偡傞偺偵偐偐傞帪娫傪 t2 偲偡傞(曅摴偼偦偺敿暘偺 t2/2偱峴偗傞偲偄偆偙偲 )丅(恾2嶲徠)
丂慏偑愳傪娸偐傜娸傊偲峴偔偲偒丄愳偼棳懍u偱棳傟偰偄傞偨傔愳娸偐傜悅捈偵弌偨偮傕傝偱傕 ut2/2 偩偗壓棳偵棳偝傟傞偙偲偵側傞丅
側偺偱恀偭捈偖恑傓偨傔偵偼偼偠傔偐傜 ut2/2 偩偗忋棳偺抧揰偵岦偐偆偮傕傝偱弌側偗傟偽側傜側偄丅偟偨偑偭偰丄
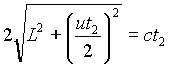 #3
#3
偐傜
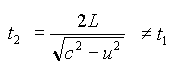 丂嘇
丂嘇
偲偄偆晽偵丄t2 偑媮傑傞丅
偦偟偰丄嘆幃偺 t1 偲斾傋偰傕傢偐傞傛偆偵 t1 偲 t2 柧傜偐偵堎側傞丅
偮傑傝丄棳傟偰偄傞愳偺拞偱偼摨偠嫍棧傪摦偔応崌偱傕丄恑峴曽岦偵傛偭偰偐偐傞帪娫偑堎側傞偲偄偆偙偲偱偁傞丅
榖偟傪岝偺応崌偵栠偡偲丄岝偵(忋婰偺愳偺傛偆偵)攠幙偑懚嵼偟丄岝偼攠幙偵懳偟偰偄偮傕摨偠懍偝偱揱傢傞偲偡傞偲丄恑峴曽岦偺堘偆岝偑摨偠偩偗偺嫍棧傪恑傓帪娫偼堎側傜側偗傟偽側傜側偄丅
偟偐偟丄尰幚偼偦偆偱偼側偐偭偨丅
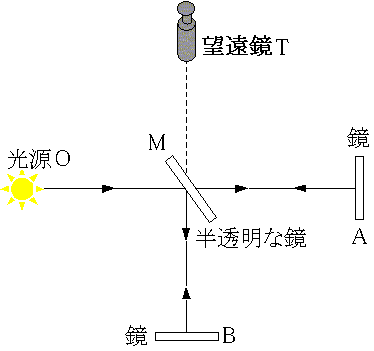
丂儅僀働儖僜儞偲儌乕儗乕偼壓恾偵帵偡傛偆側憰抲傪巊偭偰丄O仺M仺A仺M仺T 偲 O仺M仺B仺M仺T 傪揱傢傞2偮偺岝慄偑崌棳偟偰偮偔傞姳徛幦#4傪朷墦嬀T偱娤應偟偨丅
 丂恾3
丂恾3
丂偙偺憰抲慡懱偼悈嬧偺忋偵晜偄偰偄偰夞揮偝偣傞偙偲偑弌棃傞丅 岝偵攠幙偑偁傞偲偡傞偲丄岞揮偲帺揮傪偟偰偄傞抧媴忋偺憰抲偼攠幙偵懳偟偰塣摦偟偰偄傞偲峫偊傜傟傞偺偱丄憰抲偺岦偒傪曄偊傞偲2偮偺岝慄偺摓払帪娫偵偼愭傎偳偺慏偺応崌偺傛偆偵嵎偑惗偠傞偙偲偵側傞丅 偦偺帪娫嵎偵傛偭偰埵憡嵎偑曄壔偡傞偨傔丄姳徛偺幦傕偢傟傞偼偢偱偁傞丅 偟偐偟丄憰抲傪偳偺傛偆側岦偒偵抲偄偰傕姳徛幦偵曄壔偼尒傜傟側偐偭偨丅 傑偨丄堦擭偺偳偺婫愡偵幚尡偟偰傕摨偠寢壥偑摼傜傟偨丅 偙偺寢壥偼丄岝偺懍偝偑恑峴曽岦傗岝尮傗娤應幰偺塣摦乮抧媴偺岞揮偲帺揮乯偵傛傜偢堦掕偱偁傞偙偲傪帵偟偰偄傞丅 偡側傢偪丄
丂亀岝偺懍偝偺應掕寢壥偼丄娤應幰傗岝尮偺塣摦偵傛傜偢堦掕偱偁傞丅亁
偲偄偆偙偲偵側傝丄岝乮堦斒偵偼揹帴攇偱偁傞乯傪揱偊傞暔幙偲偟偰偺攠幙乮僄乕僥儖乯偺懚嵼偼斲掕偝傟偨丅
揹帴攇傪揱偊傞揹応偲帴応偼乮僄乕僥儖偺傛偆側乯暔幙偵晅懏偡傞惈幙偱偼側偔丄嬻娫乮恀嬻乯偺惈幙偱偁傞偙偲偵側偭偨丅
偙偺堦掕側恀嬻拞偺岝偺懍偝傪丄廗姷揑偵 c 偲彂偔丅
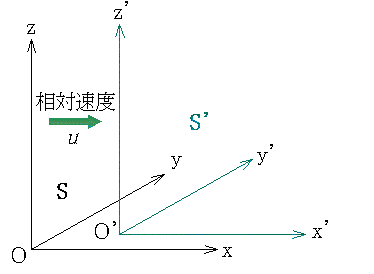
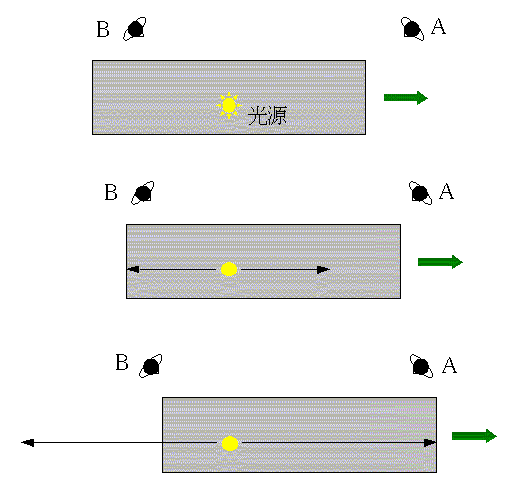
丂僯儏乕僩儞偺抸偄偨屆揟椡妛#5偱偼嵗昗宯#6 O-xyz乮埲壓丄俽宯偲屇傇乯偑姷惈宯側傜#7丄偙傟偵懳偟偰堦掕偺憡懳懍搙 u 偱摦偄偰偄傞嵗昗宯 O'-x'y'z'乮埲壓丄俽'宯偲屇傇乯傕姷惈宯偱偁傞丅 傾僀儞僔儏僞僀儞偼偙偺帠幚偲岝懍偑堦掕偱偁傞偲偄偆帠幚丄偡側傢偪
丂(1)丂偁傞姷惈宯偵懳偟偰堦掕偺懍搙偱塣摦偡傞嵗昗宯偼姷惈宯偱偁傞丅
丂(2)丂慡偰偺姷惈宯偱岝偺懍偝偼偦偺恑峴曽岦偵傛傜偢堦掕偱偁傞丅
偲偄偆俀忦審傪暔棟妛偺婎杮揑尨棟偲峫偊偨丅
恾4偺2偮偺姷惈宯 俽, 俽' 撪偱偺暔懱偺懍搙傪偦傟偧傟 v, v' 偲偡傞丅
 丂恾4
丂恾4
屆揟椡妛偱偼
丂v' 亖 v 亅 u丂丂丂丂丂嘊
偲偄偆娭學偑偁傞偺偱丄岝偺懍偝傕偙偺娭學偵廬偆偲偡傞偲丄忋偺俀忦審偼椉棫偟側偄丅 岝偺懍偝偼堦掕偲寛傑偭偰偄傞偼偢側偺偵丄忋幃偱偼岝懍偑嵗昗宯偵傛偭偰 n 偩偗堘偆偙偲偵側偭偰偟傑偆丅 丂屆揟椡妛偱偼憡懳塣摦偟偰偄傞2偮偺姷惈宯俽偲俽'偱偼嫟捠偺帪寁偑巊偊丄摨偠傛偆偵帪娫偑棳傟偰偄偔偲峫偊偰偄偨丅 備偊偵俀偮偺姷惈宯偺帪崗偼摨偠偱 (t = t')丄
丂x' = x - ut,丂丂y' = y,丂丂z' = z,丂丂t = t'丂丂丂丂丂嘋
偐傜嘊幃偑摫偐傟傞丅#8
丂偙偺傛偆偵傾僀儞僔儏僞僀儞偼丄俀偮偺姷惈宯俽偲俽'偱偼嫟捠偺帪寁偑巊偊偢丄t 偲 t' 偼摨偠偱偼側偄偲偡傟偽偙偺柕弬偑夝寛偝傟傞偙偲傪帵偟偨丅
傾僀儞僔儏僞僀儞偺憡懳惈尨棟偲屇偽傟傞忋婰偺俀忦審偵婎偯偄偨棟榑傪摿庩憡懳惈棟榑偲偄偆丅
丂摿庩憡懳惈棟榑偵傛偭偰擔忢惗妶偺宱尡偲偼堎側傞傛偆側偙偲偑梊尵偝傟傑偟偨丅
[摦偄偰偄傞帪寁偺抶傟]
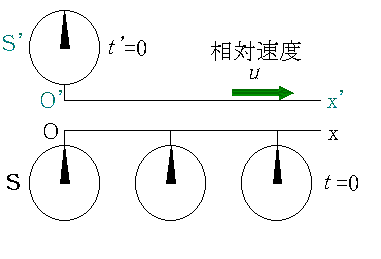
丂偁傞姷惈宯俽偺x幉忋偵偨偔偝傫偺帪寁暲傋偨忬懺傪梡堄偟傑偡丅 偦偟偰丄俽宯偺娤應幰偵偼偙傟傜偺帪寁偼慡偰摨偠帪崗 t 傪帵偡傛偆偵挷惍偟偰偍偒傑偡丅 傑偨丄俽'宯偺尨揰偵 O' 偵傕帪寁偑屌掕偟偰偁傝丄偙偪傜偼帪崗 t' 傪帵偟偰偄傞丅 偦傟偧傟偺宯偺尨揰丄O 偲 O' 偑摨偠強偵偁傞偲偒丄慡晹偺帪寁傪僛儘偵崌傢偟偰偍偔丅 偮傑傝丄t = 0 , t' = 0 偱偁傞丅
 丂恾5
丂恾5
俽'宯偼俽宯偵懳偟偰丂x 幉曽岦傪懍搙 u 偱摦偄偰偄傞偺偱丄俽'宯偺尨揰 O' 偼 t 昩屻偵 ut 偩偗摦偄偨偲偙傠偵偁傞丅
偙偺偲偒俽'宯偺尨揰 O' 偵偁傞帪寁偼
 丂丂丂丂嘍
丂丂丂丂嘍
偲偄偆傛偆偵昞偝傟丄俽'宯偱偺帪崗 t' 偼俽宯偱偺帪崗 t傛傝傕抶傟偰偄傞偙偲傪帵偟偰偄傞丅#9
 丂恾6
丂恾6
偦偺徹柧傪埲壓偵偟傑偡丅
丂帪娫傪應傞庤抜偲偟偰岝偺捠夁偟偨嫍棧傪巊偄傑偡丅
崅懍搙偱恑傓揹幵偺拞傪墶愗偭偰墲暅偡傞岝傪峫偊傑偡丅
揹幵偺幵椉暆傪 L 偲偡傞偲丄揹幵偺拞偱尒偨応崌丄岝偺憱偭偨嫍棧偼 2L 偱偡丅乮恾偼楍幵傪忋偐傜尒偨傕偺乯
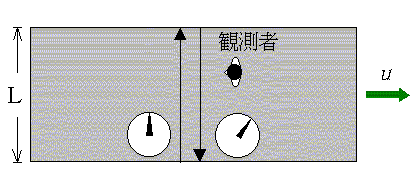 丂恾7
丂恾7
師偵抧忋偐傜尒偨応崌丄揹幵偼懍偝 u 偱憱偭偰偄傞偺偱岝偺憱偭偨嫍棧偼
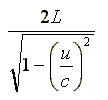 偱偡丅乮嘇幃嶲徠丄峫偊曽偼愳傪棳傟傞慏偲摨條乯#10
偱偡丅乮嘇幃嶲徠丄峫偊曽偼愳傪棳傟傞慏偲摨條乯#10
 丂恾8
丂恾8
揹幵偺拞偱尒偨応崌乮恾7乯丄岝偺墲暅偡傞帪娫 t' 偼嫍棧偐傜懍偝傪妱偭偰 t' = 2L / c 偲偄偆偙偲偑偡偖偵傢偐傞丅 抧忋偐傜尒偨応崌乮恾8乯丄岝偺墲暅偡傞帪娫 t 偼 #10 偵傕彂偄偨傛偆偵嘇幃偵偁偨傞丅 偟偨偑偭偰丄岝偺墲暅偡傞帪娫偵偮偄偰埲壓偺傛偆偵擇偮偺幃偑摫偐傟偨偺偱偡丅
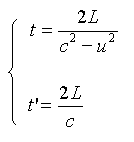 丂丂丂丂嘐
丂丂丂丂嘐
偙偺楢棫曽掱幃傪夝偔偲乮 L 傪徚嫀乯丄愭傎偳偺嘍幃
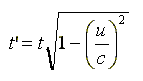 丂丂丂丂嘍
丂丂丂丂嘍
偑媮傑傞丅偡側傢偪偙偺幃偼丄摦偄偰偄傞帪寁偼抶偔恑傓傛偆偵尒偊傞偙偲傪昞偟偰偄傞丅#9
丂偙偺傛偆偵丄摦偄偰偄傞帪寁偼抶偔恑傓傛偆偵尒偊傞偺偱丄屳偄偵憡懳塣摦傪偡傞娤應幰偼丄堎側偭偨俀偮偺応強偱婲偙偭偨尰徾偑摨帪崗偵婲偙偭偨偐偳偆偐堄尒傪堦抳偝偣傜傟側偄丅
偙偺偙偲偼丄摨帪崗偺憡懳惈偲尵傢傟傑偡丅
偙偺尨場偼忣曬傪揱払偡傞揹帴攇乮岝乯偺懍偝偑桳尷偩偐傜偱偡丅#11
<椺>丂岝懍偵嬤偄懍偝偱摦偔揹幵偑偁傞偲偟傑偡丅 揹幵偺嵟慜晹偲嵟屻晹丄偍傛傃抧忋偵偄傞俀恖偺娤應幰偺崌寁係恖偺娤應幰傪峫偊丄楍幵偺拞墰偱岝偑敪偣傜傟偨偲偒偺偙偲傪峫偊傑偡丅丂 抧忋偺娤應幰俙丆俛偼丄岝偑揹幵偺嵟慜晹偲嵟屻晹偵払偟偨弖娫偵揹幵偺嵟慜晹偲嵟屻晹偺恀墶偵偄傞傛偆偵棫偭偰偄傞丅 楍幵撪偺娤應幰俠丆俢偼岝偑揹幵偺嵟慜晹偲嵟屻晹偵摨帪偵摓払偡傞偲姶偠傞丅乮恾9丄忋偐傜壓偺弴偵帪娫偑恑傫偱偄傞忬懺乯
 丂恾9
丂恾9
抧忋偺娤應幰俙丆俛偼丄岝偑曻弌偝傟偨抧揰偑俀恖偺恀傫拞傛傝屻傠婑傝側偺偱丄岝偼嵟屻晹偵偮偄偨屻丄彮偟抶傟偰嵟慜晹偵摓払偟偨偲姶偠傞偼偢偱偁傞丅乮恾10丄忋偐傜壓偺弴乯
 丂恾10
丂恾10
偙偺椺偼丄俀偮偺尰徾偑摨帪崗偵婲偙偭偨偐斲偐偼嵗昗宯偱堎側傞偲偄偆摨帪崗偺憡懳惈偺堦椺偱偡丅
[屌桳帪]
丂塣摦偟偰偄傞暔懱偺崗傓帪崗傪偦偺暔懱偺屌桳帪偲傛傃傑偡丅
偁傞姷惈宯偵懳偟偰懍偝 u 偱摦偄偰偄傞暔懱偺屌桳帪偺恑傒曽偼丄偦偺姰惉宯偵惷巭偟偰偄傞帪寁偺恑傒曽偺
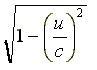 攞偱偡丅
攞偱偡丅
丂塣摦偟偰偄傞帪寁偑備偭偔傝恑傓偲偄偆憡懳惈棟榑偺寢榑偼幚尡揑偵専徹偝傟偰偄傑偡丅
晄埨掕側尨巕妀傗慺棻巕丄屌桳帪偱應偭偨偲偒堦掕偺暯嬒庻柦偱曵夡偟傑偡丅
偨偲偊偽丄惷巭偟偰偄傞儈儏乕棻巕偺暯嬒庻柦偼 2.2亊10 -6 [昩] 偲偄偆帪娫偱偡丅
偙傟偵懳偟偰丄懍偝 u 偱摍懍捈慄塣摦傗摍懍墌塣摦偟偰偄傞儈儏乕棻巕偺暯嬒庻柦偼丄惷巭偟偰偄傞応崌偺
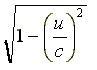 攞偱偁傞偙偲偑妋偐傔傜傟偰偄傑偡丅
攞偱偁傞偙偲偑妋偐傔傜傟偰偄傑偡丅
[儘乕儗儞僣廂弅]
丂懍偝 u 偱抧忋傪崅懍塣揮偟偰偄傞揹幵偺拞偺帪寁偼丄抧昞忋偺嫍棧俴傪娫偵帪娫 俴/u 偱偼側偔丄
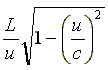 偺帪傪崗傓傛偆偵尒偊傞丅乮恾6嶲徠乯
偟偨偑偭偰丄揹幵偺塣揮庤偵偼抧昞忋偺嫍棧俴偼俴偱偼側偔
偺帪傪崗傓傛偆偵尒偊傞丅乮恾6嶲徠乯
偟偨偑偭偰丄揹幵偺塣揮庤偵偼抧昞忋偺嫍棧俴偼俴偱偼側偔
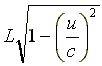 偵弅傫偱尒偊傞偙偲偵側傞丅
偡側傢偪丄懍偝 u 偱摦偄偰偄傞暔懱偼丄惷巭偟偰偄傞応崌偵斾傋偰丄塣揮曽岦偺挿偝偑
偵弅傫偱尒偊傞偙偲偵側傞丅
偡側傢偪丄懍偝 u 偱摦偄偰偄傞暔懱偼丄惷巭偟偰偄傞応崌偵斾傋偰丄塣揮曽岦偺挿偝偑
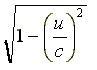 攞偵弅傫偱尒偊傑偡丅
偙傟傪儘乕儗儞僣廂弅偲尵偄傑偡丅
偪側傒偵丄暔懱偺塣摦曽岦偵悅捈側曽岦偺挿偝偼惷巭偟偰偄傞偲偒偲摨偠偵尒偊傞丅
攞偵弅傫偱尒偊傑偡丅
偙傟傪儘乕儗儞僣廂弅偲尵偄傑偡丅
偪側傒偵丄暔懱偺塣摦曽岦偵悅捈側曽岦偺挿偝偼惷巭偟偰偄傞偲偒偲摨偠偵尒偊傞丅
[塣摦検曐懚懃偲憡懳惈棟榑]
[幙検偲僄僱儖僊乕]
丂偛懚偠丄儕儞僑偑棊壓偡傞偺偼壗屘偐丠偲偄偆媈栤偐傜惗傑傟偨傕偺偱丄暔懱偺塣摦偼偦偺幙検m丄壛懍搙a丄偐偐傞椡F偺俁偮偺僷儔儊乕僞偱昞偝傟傞偲偄偆傕偺丅
丂F = m 亊 a
#2丂帪娫丄嫍棧丄懍偝
丂偁傞暔懱偺懍偝傪媮傔傞偲偒丄嫍棧偲帪娫偑梌偊傜傟偰偄傟偽
[懍偝]亖[嫍棧]亐[帪娫]
偱丄媮傔傞偙偲偑弌棃傞丅
偙偺応崌丄嵍曈偵帪娫傪帩偭偰偒偨偺偱
[帪娫]亖[嫍棧]亐[懍偝]
偲丄彂偒捈偝傟傞丅
偮傑傝丄慏偺恑傓嫍棧L傪懍偝偱妱傞偙偲偱丄L傪恑傓偺偵偐偐傞帪娫傪媮傔傞偙偲偑弌棃丄忋傝偲壓傝傪懌偡偙偲偵傛偭偰墲暅偵偐偐傞帪娫傪媮傔偨傢偗偱偡丅
#3丂捈妏嶰妏宍偺婎杮揑惈幙
丂捈妏嶰妏宍偱偼丄俁曈偺偆偪俀曈偺挿偝偑傢偐偭偰偄傟偽巆傝偺侾曈傪梕堈偵媮傔傞偙偲偑弌棃傞丅
捈妏嶰妏宍偺応崌丄埲壓偺娭學偑惉傝棫偮偐傜偱偁傞丅
丂(幬曈)2 = (曈1)2 + (曈2)2
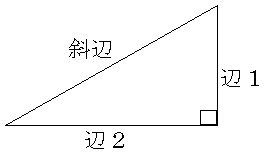
崱偺応崌丄廲偺曈偑愳偵棳偝傟傞挿偝丄墶偺曈偑愳暆丄幬曈偑慏偺幚嵺偵恑傓嫍棧丅
偟偨偑偭偰丄忋偺嶰妏宍偲摨條偵
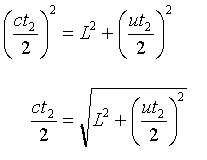
偲側傝丄嵟廔揑偵嘇幃偑媮傑傞丅
#4丂姳徛幦
丂攇偵偼埵憡偲偄偭偰丄侾廃婜撪偱偺攇偺恑峴抜奒傪帵偡検偑偁傞丅
偙偺埵憡偼帪娫偲偲傕偵曄壔偡傞検偱偁傞丅
2偮偺摨偠攇挿偺岝偑廳側傞偲偒丄偍屳偄偺埵憡偑堎側傞偲廳偹崌傢偣偵傛傝丄攇傪嫮傔崌偆偲偙傠偲懪徚偟崌偆偲偙傠偑惗傑傟傞丅
偙偺傛偆側嫮庛偑幦偲偟偰尰傢傟傞丅
偦偟偰丄幦偺僷僞乕儞偼攇偺姳徛偺巇曽丄偮傑傝埵憡偺嵎偵傛偭偰曄傢偭偰偔傞丅
媡偵尵偊偽丄埵憡乮帪娫乯偵嵎偑側偗傟偽幦偺僷僞乕儞偼曄傢傜側偄丅
#5丂屆揟椡妛
丂偼偠傔偵傕弎傋偨傛偆偵丄堦斒偵暔懱偺塣摦偼僯儏乕僩儞偺塣摦朄懃偵傛偭偰婰弎偝傟傞丅 偟偐偟丄垷岝懍側塣摦傗丄旝帇揑側悽奅偺塣摦偼偦偺塣摦曽掱幃偱偼惓妋偵婰弎偱偒側偔側偭偰偔傞丅 偦偙偱丄尰戙偱偼検巕椡妛傑偱敪揥偟偨尰戙暔棟妛偑峔抸偝傟偰偄傞丅 偦偺尰戙暔棟偵懳偟偰丄僯儏乕僩儞偑抸偄偨椡妛傪屆揟椡妛偲屇傇丅 堦斒揑偵偼崅峑惗偱廗偆椡妛偑屆揟椡妛偱偡丅
#6丂嵗昗宯
丂嵗昗偭偰壗丠偭偰暦偐傟傞偲崲偭偰偟傑偆丅壗偲側偔傢偐傞偱偟傚丠偙偭偪傕愢柧偟偯傜偄傫偩偗偳丄偪傖傫偲尵偆偲偙傫側姶偠偱偡丅
丂俁師尦嬻娫偺応崌丄偳偙偐偵尨揰偲偄偆婎弨偲側傞揰傪寛傔丄俁杮偺捈峴偡傞悢捈慄偺岎揰偑尨揰偵側傞傛偆偵偡傞丅
偦偆偡傞偲嬻娫偺偁傜備傞揰偼丄偙傟傜俁杮偺悢捈慄偺栚惙傝偺悢抣偺慻傒崌傢偣偱昞偡偙偲偑弌棃傞丅
偦傟偱嵗昗宯偲偼丄嵗昗偺庬椶丄尨揰傗幉偲偄偭偨傕偺偺憤徧丅
丂偙偺応崌 O-xyz 偲偼丄尨揰偑 O 偱3偮偺幉傪偦傟偧傟 x,y,z 偲偟偨嵗昗宯丄偲偄偆堄枴偱偡丅
#7丂姷惈宯
丂僯儏乕僩儞偺塣摦偺戞堦朄懃偼丄椡傪壗傕庴偗偰偄側偄暔懱偼惷巭偟懕偗傞偐丄傕偟偔偼摍懍捈慄塣摦傪峴偆偲偄偆傕偺偱偟偨丅 偙偺戞堦朄懃偼姷惈偺朄懃偲傕屇偽傟丄偙傟偑惉傝棫偮嵗昗宯傪姷惈宯偲偄偆丅 忋偺榖偱偼丄偁傞嵗昗宯偱姷惈偺朄懃偑惉傝棫偮側傜丄偦傟偵懳偟偰摍懍塣摦傪偡傞嵗昗宯偱傕惉傝棫偮偼偢偱偁傞丄偲偄偆偙偲傪尵偭偰偄傞偺偱偡丅 偦傟偼丄慡偰偑摍懍塣摦偟偰偄傞偺偱偁傟偽懍偝傪嵎偟堷偒偟偨偲偙傠偱摍懍塣摦偱偁傞偙偲偵曄傢傝偼側偄偐傜偱偡丅
#8丂旝暘
丂椡妛偱偼丄埵抲傪昞偡娭悢傪帪娫偱旝暘偡傞偲懍搙偵側傞丅
偮傑傝丄埵抲傪昞偡娭悢傪 x 偲偟偨偲偒
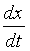
偲偄偆傕偺偑懍搙傪昞偡丅
傑偨丄懍搙傪帪娫旝暘偡傞偲壛懍搙偵側傞丅
偙傟偼 x 傪俀奒旝暘偡傞偙偲偵側傝
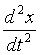
偲彂偐傟傞丅
丂旝暘偡傞懳徾偲側傞娭悢偲摨偠傕偺偱旝暘偡傞応崌偼丄扨弮側悢帤偺僷僘儖偺傛偆側傕偺偱偁傞丅 偙偺旝暘傪偡傞偲丄旝暘偝傟傞娭悢偺師悢偑學悢偲偟偰偐偐傞偩偗偱偁傞丅 椺傪帵偡偲丄t2 傪 t 偱旝暘偟偨偲偒丄師悢偺俀偑 t 偺慜偵偐偐傝丄偦偺師悢偼侾偮壓偑傞丅 偮傑傝丄乮 娭悢 t 偼俀忔偐傜侾忔偲側傝乯夝偼 2t 偲側傞丅 t3 側傜 3t2 偲側傞丅
#9丂t 亜 t'
丂嘍幃偐傜丄側偤 t' 偑 t 傛傝傕抶傟偰偄傞丄偡側傢偪彫偝偄抣傪偲傞偲尵偊傞偺偐傪愢柧偟傑偡丅
傑偢丄儖乕僩偺崁偑偑側偗傟偽 t' = t 側傢偗偱儖乕僩偺拞恎偑 t' 偺戝彫傪寛傔偰偄傞偙偲偑傢偐傞偲巚偄傑偡丅
偝傜偵儖乕僩撪偱偼丄侾偐傜壗偐傪堷偄偰偄傞傢偗偱偡丅
偙偺堷偄偰偄傞傕偺偑側偗傟偽儖乕僩侾偲側傝丄寢嬊 t' = t 偱偁傞偨傔偦偺堷偄偰偄傞傕偺偵拲栚偡傞昁梫偑偁傝傑偡丅
偙偙偱丄u 偼俽'宯偺摦偔懍搙丄c 偼岝偺懍偝偱偡丅
岝傛傝懍偔摦偔偙偲偼弌棃側偄偲偡傞偲丄u 偼 昁偢 c 傛傝彫偝偔側傝傑偡丅
偟偨偑偭偰丄偙偺暘悢偼侽偐傜侾偺抣傪偲傝摼傞傢偗偱偡丅
備偊偵丄儖乕僩偺拞恎傕侽偐傜侾偺抣丅
偦傟傪 t 偵偐偗傟偽 t'偼彮側偔偲傕 t 傛傝戝偒偔側傞偙偲偼側偔 u 亙 c 偺応崌丄t' 偼 t 傛傝彫偝偔側傝傑偡丅
丂偮偄偱偵尵偆偲丄偙偺幃偐傜偼岝懍偱摦偔宯偵懳偟偰偼乮 u = c 偺偲偒乯t' =0 偲側傝帪娫偑巭傑傞偲偄偆偙偲偑尵偊傞丅
#10
丂慜偺応崌偲摨條偵峫偊傞偲丄愭傎偳偺慏傪岝偵丄愳偺棳傟傪楍幵偵抲偒偐偊傞偙偲偑弌棃傞丅 偦偆偡傞偲丄嘇幃偺 t2 傪 t 偲偡傞偙偲偱丄偙偺 t 偼抧忋偐傜尒偨岝偑楍幵傪墲暅偡傞帪娫傪昞偡偙偲偵側傞丅 偙偺帪娫偵岝偺懍偝 c 傪偐偗偰傗傟偽丄忋婰偺傛偆偵岝偺憱偭偨嫍棧偑媮傑傞丅
#11
丂偙傟偼#9偱弎傋偰偄傞峫偊曽傪巊偆偺偩偑丄c 偑柍尷偩偲偡傞偲 u 偼 c 偵懳偟偰忢偵彫偝偄傢偗偱丄偝傜偵偳傟傎偳偺懍偝傪帩偭偰偟偰傕柍尷偵懳偟偰偼庢傞偵懌傜側偄戝偒偝偲側傞丅 備偊偵丄偁偺儖乕僩偺拞恎偺 u / c 偲偄偆偺偼僛儘偲峫偊傞偙偲偑弌棃丄t' = t 偲側偭偰帪娫偺偢傟偼惗偠側偄偙偲偵側傞丅 偟偐偟丄尰幚偱偼岝偺懍偝偑桳尷偱偁傞偨傔丄摦偄偰偄傞帪寁偵抶傟偑惗偠傞偙偲偼柶傟側偄丅